Vibration Control in Microelectronics, Optics and Metrology
Negative-Stiffness-Mechanism Vibration Isolation Systems

David L. Platus

Minus K Technology
11775 Gateway Boulevard, #6, Los Angeles, CA 90064 USA

ABSTRACT

A new type of vibration isolation system* offers significant improvement in performance compared with current state-of-the-art systems. The system uses negative-stiffness mechanisms to cancel the stiffness of a spring suspension. Reduction in stiffness magnifies the damping inherent in the system creating a practical means for achieving high hysteretic damping. The result is a simple, compact 6-DOF passive isolation system capable of system resonant frequencies below 0.2 Hz and first isolator resonances above 100 Hz. Resonant transmissibilities below 1.4 can be achieved with transmissibilities at the higher frequencies close to that of the ideal undamped system. The negative-stiffness mechanisms can cancel the stiffness of power cables, hoses or other lines connected to payloads. This paper develops the theory, describes typical configurations and summarizes lest data with prototype systems.

1. THEORY OF OPERATION

1.1 Vertical-motion isolation
A typical vertical-motion isolator uses a conventional spring to support the payload weight and a negative-stiffness mechanism (NSM) ("snap-through" or "over-center" mechanism) to cancel some or all of the stiffness of the spring, thereby producing low or zero net vertical stiffness. This approach has been used successfully to simulate zero gravity in the testing of large space structures (1-2). Its use in 6-DOF vibration isolation systems as described in this paper is unique.

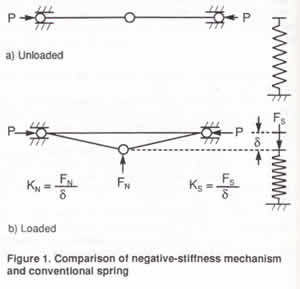An NSM is illustrated in Figure 1 and is compared with a conventional spring. The NSM consists of two bars hinged at the center, supported at their outer ends on pivots which are free to move horizontally, and loaded in compression by opposing forces P. For this example, motions are constrained to the plane of the paper. In Figure l(a) the bars arc aligned and arc in a stale of unstable equilibrium (the center position of the NSM). In Figure l(b), the center hinge is displaced downward an amount and is held in equilibrium by the force FN which opposes the displacement. For small values of , a linear relationship exits between FN and which is expressed by the negative stiffness KN. The behavior of a conventional spring is also shown, unloaded in Figure l(a) and deflected an amount by the force FS in Figure l(b). Here, the force FS acts in the direction of the displacement to hold the deflected spring in equilibrium, and the ratio of FS to is the positive stiffness KS.

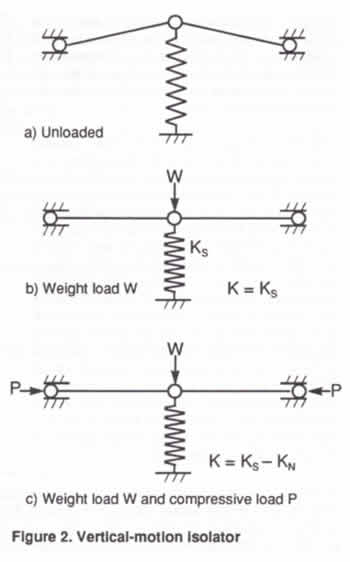
The spring and the NSM are combined to produce the vertical-motion isolator shown in Figure 2. The isolator is shown unloaded in Figure 2(a). In Figure 2(b), a weight load W deflects the spring to the center position of the isolator. The vertical stiffness of the system in Figure 2(b) is the spring stiffness. In Figure 2(c), forces P arc applied to the bars, creating the NSM which cancels some or all of the spring stiffness. This is the operating condition of the system. The resulting isolator stiffness is K = KN - KS, and can be made to approach zero while the weight load is still supported by the spring of stiffness KS. Flexures can be used in place of the hinged bars and offer advantages in practical systems. The compressive load P can be applied by various means such as a loading screw or a piezoelectric device.

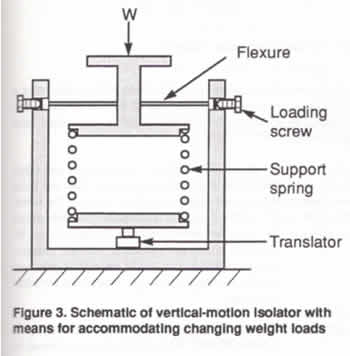
A schematic of a vertical-motion isolator with means for accommodating changing weight loads is shown in Figure 3. This isolator uses flexures and loading screws. A translator raises and lowers the base of the spring in order to maintain the center position of the isolator within specified limits. Automatic leveling can be provided by controlling the translator with limit switches or with signals from a displacement transducer.

1.2 Horizontal-motion isolation
Horizontal-motion isolation can be provided by a set of flexible columns or beam-columns that behave as springs combined with NSMs. This is illustrated in Figure 4 with a planar example in which a payload is supported on two flexible columns. The displaced position in response to horizontal excitations is shown in Figure 4(a). The payload displaces without significant rotation because the columns are very stiff in the vertical direction compared with their stiffness in the horizontal direction. The horizontal stiffness can be made near zero by designing the columns to be loaded to approach their critical buckling loads, thereby producing very low natural frequencies for horizontal vibrations.

The buckling mode of the system is also generally indicated by the deformed shape illustrated in Figure 4(a). As the system collapses, the payload displaces horizontally and downward. The addition of stops to limit horizontal displacements produces a system that is fail-safe against collapse due to inadvertent overload. Limiting the horizontal displacements of the payload to small values changes the buckling mode and increases the buckling strength nominally by a factor of four. Of course, the system does not isolate when the payload is against the stops.

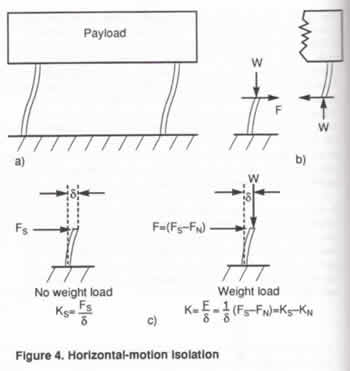This approach makes use of the "beam-column effect," i.e., the reduction in bending stiffness of a beam-column due to the axial load. The beam-columns in the isolation system of Figure 4 are equivalent to two fixed-free columns, as illustrated in Figure 4(b). Consider the fixed-free column of Figure 4(c). Without weight load, the beam-column is simply a cantilever beam with lateral (horizontal) end load, and acts as a spring with horizontal stiffness KS. The weight load W produces bending moments on the laterally-loaded beam, proportional to the deflection 8. so that less lateral force is required to produce 8. This behavior is equivalent to that of a spring of stiffness KS combined with an NSM having negative stiffness of magnitude KN that subtracts from the stiffness KS. As W approaches the critical buckling load, K^ approaches Ks and the net horizontal stiffness of the beam-column approaches zero.

A schematic of a horizontal-motion isolation system that passively accommodates changing weight loads while maintaining a fixed isolation system natural frequency is shown in Figure 5. The payload is supported on two sets of flexible columns pre-loaded with axial load Q. Each set has an upper and a lower column. The lower column supports its part of the weight load plus the axial pre-load. The upper column supports only the axial pre-load.

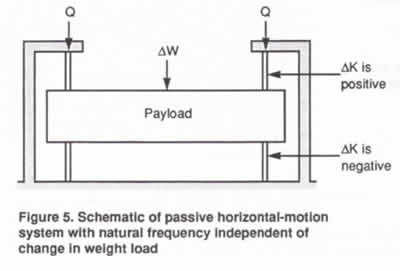Consider, for example, the effect of an increase in payload weight. Because of the axial flexibility of the columns and other flexibility in the system, the increase in payload weight increases the axial load on the lower column and decreases (he axial load on the upper column. The increase in axial load on the lower column increases the negative-stiffness effect in the lower column reducing its horizontal stiffness; the decrease in axial load on the upper column decreases the negative-stiffness effect in the upper column increasing its horizontal stiffness. By proper sizing of the upper and lower columns, the system can be designed so that the horizontal stiffness changes in proper proportion to the change in payload weight so that the natural frequency remains unchanged.

Changes in the pre-load Q change the negative-stiffness effect in the upper and lower columns in the same direction, thereby providing an independent means for adjusting the system horizontal stiffness and resonant frequency.

1.3 Damping
Damping is required to limit the isolation system resonant responses. Reduction in stiffness with the NSM magnifies the damping inherent in the system, creating a practical means for achieving high hysteretic damping. High hysteretic damping is more desirable than high viscous damping because it can limit resonant responses without significantly reducing isolation efficiencies at the higher frequencies. 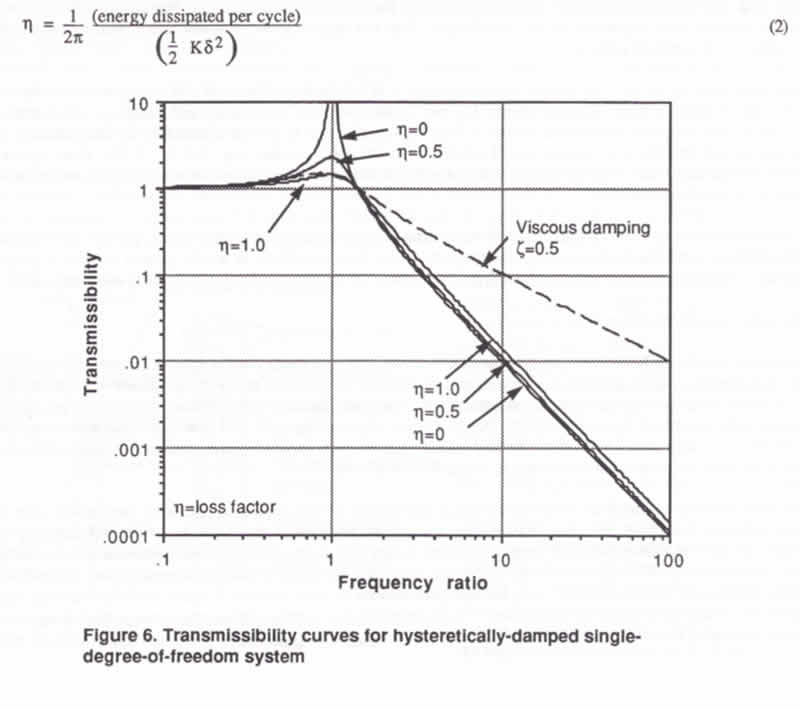This is illustrated by the transmissibility curves shown in Figure 6 for a hysteretically-damped system. For example, with a loss factor of 1.0, the resonant transmissibility is 1.4 and the transmissibilities at higher frequencies deviate only slightly from the ideal undamped curve. For comparison, a transmissibility curve is shown for a viscously-damped system that gives the same resonant transmissibility of 1.4 (the viscous critical damping ratio is 0.5). The difference in transmissibilities between the viscously-damped and the hysteretically -damped systems at the higher frequencies is quite dramatic considering the log scale used in the figure.

Magnification of the damping by reduction of the stiffness with the NSM can be explained as follows: Consider an ordinary spring with stiffness Kg and loss factor 1)5, supporting a mass and vibrating harmonically with displacement amplitude 5. The loss factor is related to the energy dissipated in the spring and the energy stored in the spring by,

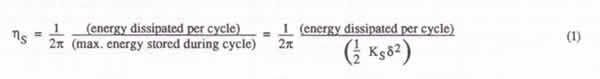
The same basic relationship applies to the isolation system whose stiffness has been reduced from Ks to K by an NSM. The resulting isolation system loss factor is.

As the net stiffness K is reduced by the NSM, the maximum elastic energy stored during the cycle, and associated with , is diminished, but the energy dissipated per cycle is not diminished. The energy dissipated per cycle is the energy dissipated t" the positive spring, and can be expressed by Equation (1). Combining Equations (1) and (2) gives.

Thus, the loss factor for the system is the spring loss factor multiplied by the ratio of spring stiffness to system net stiffness. It is also equal to the spring loss factor multiplied by the square of the ratio of system resonant frequency s, based on the spring stiffness, to the system resonant frequency based on the reduced stiffness.

A large magnification in damping is possible in a typical NSM isolation system. For example, consider a system in which the positive springs alone give a resonant frequency of 5 Hz (corresponding to Figure 2(b)), and with the NSM, a resonant frequency of 0.5 Hz. According to Equation (3) the isolation system loss factor is equal to the spring loss factor multiplied by 100. For example, one percent structural damping in the spring would produce 100% structural damping in the isolation system.

There are benefits from adding damping to the suspension system, particularly in the form of high-damping viscoelastic materials. Consider a suspension of steel springs and a viscoelastic damper. The stiffness of the system is the sum of the spring stiffness and the damper stiffness, but essentially all of the damping comes from the viscoelastic damper. By adding negative stiffness with an NSM equal in magnitude to the stiffness of the steel springs, the resulting suspension behaves dynamically as though the payload were suspended on only the damper. With this approach, very low resonant frequencies and high damping can be achieved in compact systems.

The damping behavior of the viscoelastic materials typically falls between the viscous and the hysteretic curves of Figure 6. Loss factors for some of these materials exceed 1.0 over certain ranges of temperature and frequency, and manufacturers are able to tailor their materials to particular ranges of interest. Materials can be produced with loss factors exceeding 1.0 at room temperatures and the low frequencies of interest for vibration isolation, e.g., 0.2 to 1.5 Hz. Thus, system resonant transmissibilities lower than 1.4 and transmissibilities at the higher frequencies close to that of the ideal undamped system can be achieved in practical systems.

The stiffness of the system can be reduced below that of the damping material alone, producing system resonant transmissibilities significantly lower than 1.4. However, under these conditions in totally passive systems a creep instability can occur. By retaining some positive stiffness from the mechanical suspension the system is made inherently stable.

1.4 Isolation system performance
The performance of real NSM isolation systems that we have built and tested closely approaches the behavior shown by the curves of Figure 6 up to frequencies at which isolator resonances (frequencies at which the isolator structure itself resonates) occur. Because these isolators arc simple, compact elastic structures, their isolator resonances arc readily predictable and can be kept al high frequencies by proper design. Design studies supported by tests with prototype isolators indicate that isolator resonances can be kept above 100 Hz in practical 6-DOF systems with isolation system resonances (frequencies at which the system of payload and suspension resonates) as low as 0.2 Hz or lower.

System resonances in the range of 0.5 to 1.5 Hz are of interest for a wide range of applications, particularly with low system resonant response, near-hysteretic-damping behavior and isolator resonances above 100 Hz. With high-damping viscoelastic materials currently available, resonant transmissibilities as low as 1.4 arc achievable with practical passive NSM isolation systems. Even better performance can be achieved with automatic centering systems utilizing actuators controlled by signals from displacement or velocity sensors. Also, because performance of these isolators is based on deformation of simple elastic structures and viscoelastic materials, performance is not degraded (as in conventional pneumatic isolators) by micro-motions typical of laboratory floors and fabrication rooms.

2. SYSTEM CONFIGURATIONS

The isolators described above for handling vertical and horizontal vibrations can be combined to produce various configurations of 6-DOF isolators and isolation systems.

2.1 Passive systems
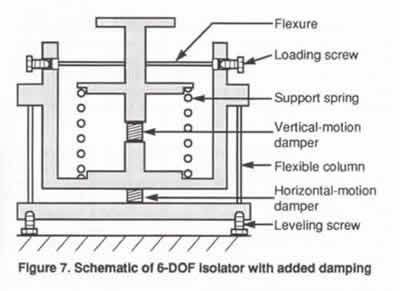A schematic of a compact passive 6-DOF isolator with added damping is shown in Figure 7. This isolator His within a somewhat conventional space, with height and diameter approximately equal. Design studies indicate size envelopes for this configuration comparable to pneumatic isolators that support the same weight loads. Other configurations depart radically from the conventional shape, including low-profile configurations that can optimize the use of limited space in laboratories and fabrication rooms.

NSM suspension systems are applicable to a very wide range of weight loads. Added weight is not required in order to achieve very low resonant frequencies, nor are the systems limited by very large weights. For example, very low frequencies can be achieved with a small isolated platform that supports a microscope and with systems that support a 3000 lb. photolithography machine or an entire fabrication room floor.

2.2 Active and automatic leveling systems
An important feature of NSM systems is their capability for stiffness and frequency adjustment through adjustment of the NSMs. For example, combining the isolators of Figures 3 and 5 with a servo system to control the vertical-motion translator can produce an automatic leveling system in which the horizontal-motion resonant frequency is insensitive to changes in payload weight. By using the servo system to control the vertical-motion NSM, the vertical-motion resonant frequency can also be made insensitive to changes in payload weight. As another example, consider step-and-repeat systems with stages that arc accelerated and decelerated (photolithography machines, CMMs, etc.) Feed-forward control systems can control the NSMs in order to stiffen the system during stage acceleration and deceleration and soften the system during exposures or measurements.

2.3 Retrofit devices
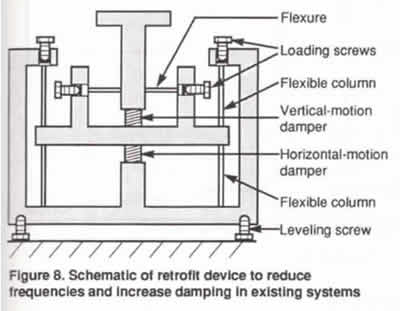
The NSMs described above can be used to retrofit existing isolation systems in order to reduce system resonant frequencies and/or to increase system damping. A schematic of a retrofit device with added damping is illustrated in Figure 8. A set of devices is connected to the existing system between the payload and ground without disturbing the system. Adjustment of the loading screws adjusts the frequencies and damping to the desired levels.

3. TEST RESULTS WITH PROTOTYPE SYSTEMS

Prototype systems have been built and tested, including an undamped vertical-motion system and damped and undamped horizontal-motion systems. An undamped horizontal-motion system is shown in Figure 9. A small 6-DOF isolated platform ii being fabricated and will soon be tested.

The undamped systems demonstrated system resonant frequencies below 0.2 Hz, as determined by visual observations. The increase in system damping with reduction in system stiffness was also apparent from observation of the decay of the free vibrations. Transmissibility tests were run on some of the horizontal-motion systems. Typical test data are shown in Figures 10 to 15. The ideal undamped curves arc shown in Figures 10 and 11 for comparison.

In the damped horizontal-motion systems the payload is supported on flexible steel columns with viscoelastic dampers connected in parallel. For the transmissibility tests, the columns were loaded close to their critical buckling loads so the systems behaved dynamically almost as though the payload were supported on only the dampers. Standard off-the-shelf damping materials were used which generally arc not optimum for the room-temperature low-frequency applications of interest. Optimum formulations of these materials can provide loss factors exceeding 1.0 and resonant transmissibilities below 1.4 at low frequencies and room temperatures.

The system of Figure 11 was first tested without the dampers and tuned to a system resonant frequency of 0.2 Hz. The dampers were then connected, raising the frequency to 0.73 Hz. Different damping materials were used for the systems of Figures 10 and 11, neither of which is optimum from the standpoint of maximum damping at system resonance.










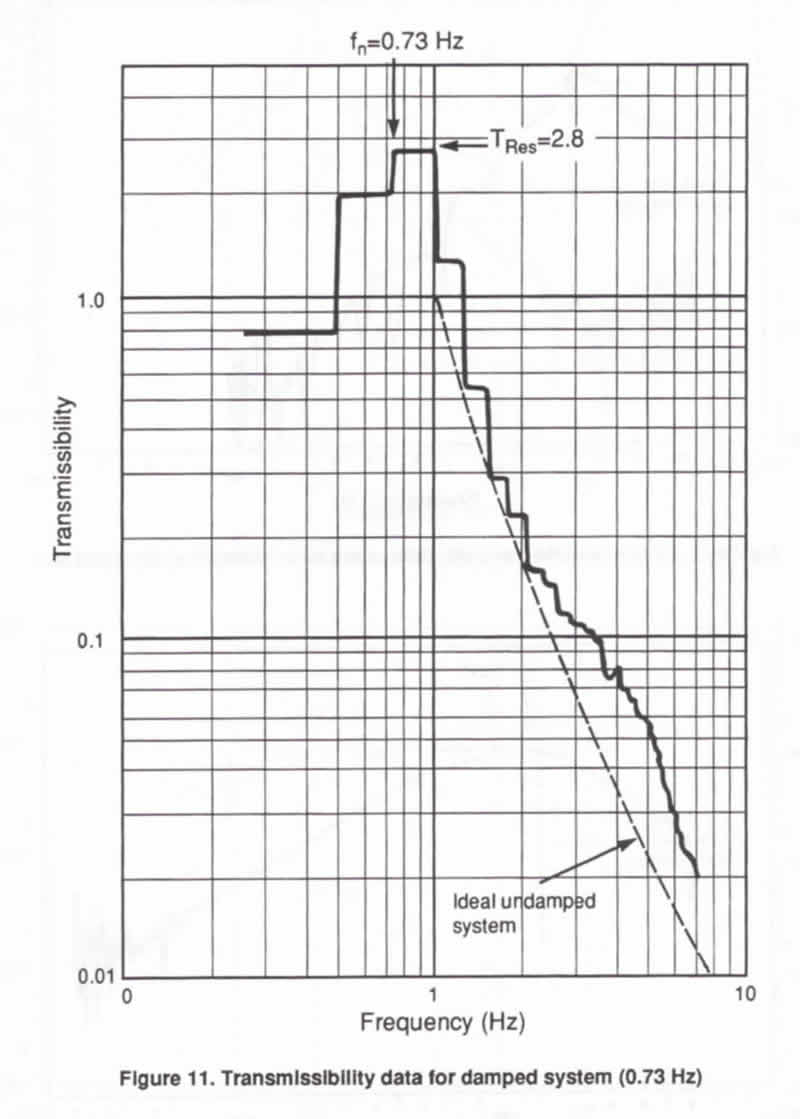
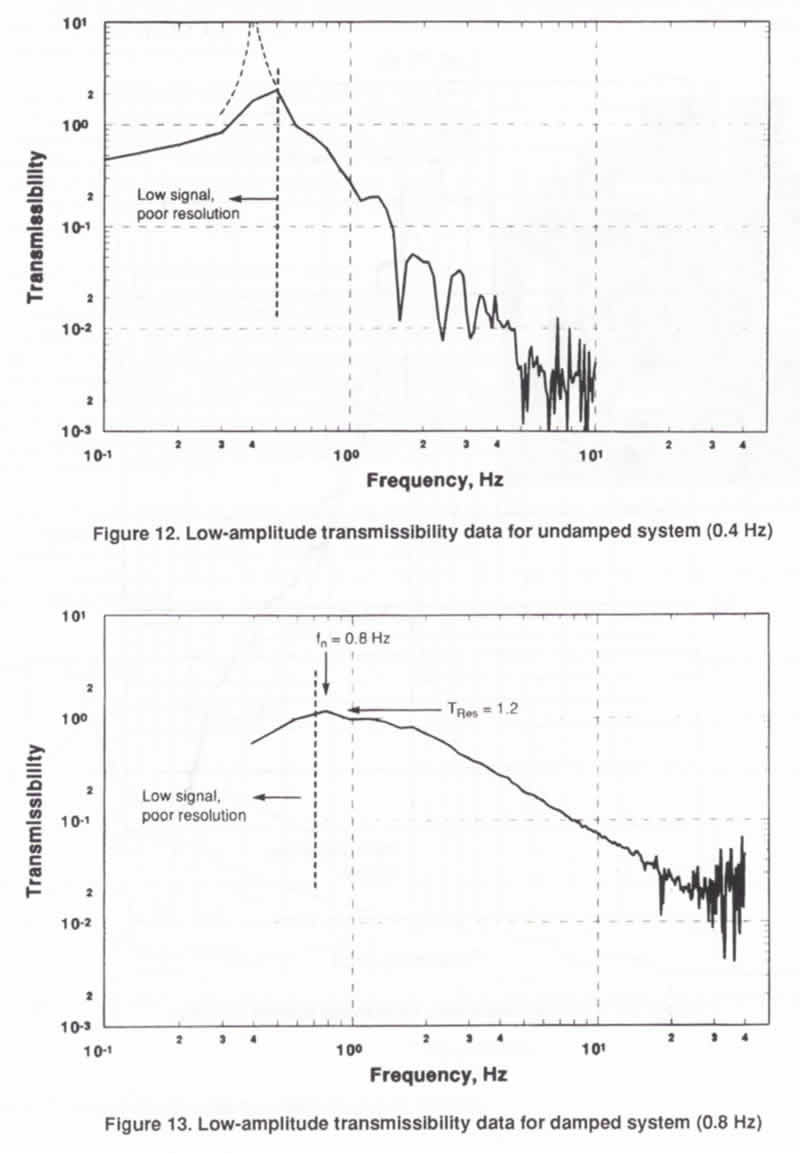
The transmissibility curves of Figures 10 and 11 were obtained using forced vibrations from electrodynamic shakers, v. inputs in the milli-g range. The curves of Figures 12 to 15 were determined from low-amplitude ambient vibrations laboratory floor with a measured input of 7.3 x 10* g RMS from DC to 15 Hz. A third damping material was used for systems of Figures 13 and 15 which does exhibit loss factors exceeding 1.0 at the system resonant frequencies. These ambient vibration transmissibility curves were measured by Dr. R.L. Nigbor of Agbabian Associates. The method used for these measurements is described in his paper, "Accurate characterization of low-level vibration environments using seismological sensors and systems," also in these proceedings.

The undamped system of Figure 12 has a resonant frequency around 0.4 Hz. Adding dampers to this system gives the system of Figure 13 with a resonant frequency of 0.8 Hz and a resonant transmissibility of 1.2. The undamped system of Figure 14 h_ a resonant frequency of 0.9 Hz. Adding dampers gives the system of Figure 15 with a resonant frequency of 4.3 Hz and a resonant transmissibility of 1.3. For the particular damping material used in the systems of Figures 13 and 15. transmissibility behavior is close to the ideal viscous curve shown in Figure 6.

4. SUMMARY OF KEY FEATURES

The following are key features of negative-stiffness-mechanism vibration isolation systems:

• Passive
• Compact
• No air
• 6-DOF isolation
• Simple automatic leveling for changing weight loads
• Can provide system resonant frequencies below 0.2 Hz and first isolator resonances above 100 Hz
• Can provide system resonant transmissibilities below 1.4 with transmissibilities at higher frequencies close to the ideal undamped system
• Not degraded by micro-motion inputs
• Can cancel the stiffness of power lines, hoses, cables, etc., connected to payloads
• Can retrofit existing systems to reduce frequencies and increase damping without disturbing the existing systems
• Isolation system stiffness can be adjusted manually or automatically
• Applicable to very small and very large payloads

5. ACKNOWLEDGEMENT

6. REFERENCES

1. R. Ikegami, et. al., "Zero-G Ground Test Simulation Methods," Proceedings of the 11th Aerospace Testing Seminar pp. 215-225, The institute of Environmental Sciences, Manhattan Beach, CA. October 11-13, 1988.
2. S.E. Woodard and J.M. Housner, "Nonlinear Behavior of a Passive Zero-Spring-Rate Suspension System," J Guidance, American Institute of Aeronautics and Astronautics, Vol. 14, No. 1, pp. 84-89, Jan.-Feb. 1991.

PDF version of this article  |  Top