
Laboratory Design - June 2018
Negative-stiffness vibration isolation at the South Pole
Wed, 06/13/2018 - 3:42pm by Jim McMahon
Lorentz invariance or symmetry, a set of fundamental frameworks that underpin modern science and physics in particular, lies at the foundation of quantum field theory (QFT) and Einstein's theory of general relativity, the two most successful theories in physics, which together describe the four fundamental forces of nature. In physics, particularly electromagnetism, the Lorentz force is the combination of electric and magnetic force on a point charge due to electromagnetic fields. While modern Maxwellian equations demonstrate how electrically charged particles and currents, or moving charged particles, give rise to electric and magnetic fields, the Lorentz force law completes that picture by describing the force acting on a moving point charge in the presence of electromagnetic fields.
The inability to incorporate gravity, however, as described by general relativity into the QFT standard model of particle physics—which very successfully combines the electromagnetic, strong and weak interactions—has led to the development of alternative theories of quantum gravity. Since many of these theories break Lorentz symmetry at some small level, experimental searches for Lorentz-violating effects could help shed light on new physics beyond the standard model, and provide clues as to the nature of quantum gravity. Lorentz violations concern the fundamental predictions of special relativity, such as the principle of relativity, the constancy of the speed of light in all inertial frames of reference, and time dilation, as well as the predictions of the standard model of particle physics.

PRINCETON’S ULTRA-PRECISE LORENTZ SYMMETRY TESTING
Some of the most precise tests relating to Lorentz symmetry are being performed by the Romalis Group at Princeton University.
“Lorentz symmetry underlies all of the known forces of nature, providing one of the few links between gravity and quantum mechanics,” said Michael Romalis, Ph.D., Professor of Physics, and head of the Romalis Group at Princeton University. “It postulates that laws of physics are invariant under rotation, and remain the same in a moving reference frame. Lorentz symmetry is also closely connected to Charge-Parity-Time (CPT) reversal symmetry that enforces the equivalence of particles and anti-particles.”
“We use ultra-high precision techniques involving polarized atomic spin to test Lorentz symmetry,” added Romalis. “The presence of Lorentz violation would appear as an effective field felt by the atoms. Presumably, this field acts as a cosmically fixed background which, from the point of view of our Earth bound experiment, fluctuates with a sidereal period as the Earth rotates in it.”
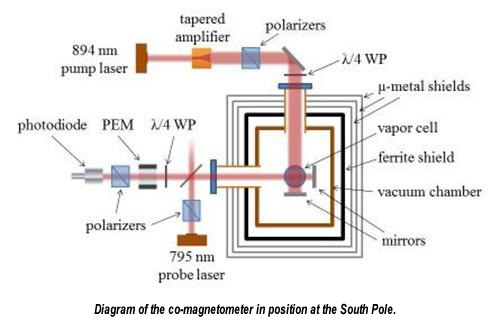
An alkali metal-noble gas co-magnetometer, enclosed within a vacuum chamber, is used in the group’s experiment to very sensitively measure fields which couple to atomic spin, while suppressing magnetic field interactions. An atomic spin co-magnetometer consists of two spin species occupying the same volume and measuring the same magnetic field. Such redundant measurements can allow one to cancel magnetic field fluctuations and focus on more interesting interactions going beyond the Standard Model of particle physics.

NULLIFYING THE EFFECTS OF THE EARTH’S ROTATION AT THE SOUTH POLE
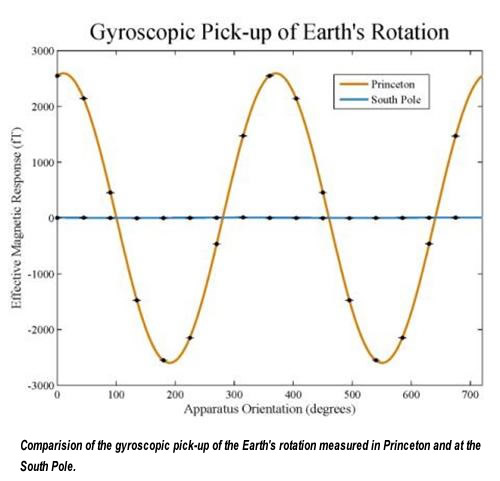
Very stringent limits on rotation and boost Lorentz violation has already been determined using measurements conducted in Princeton. However, a significant systematic effect limiting further improvements was the gyroscopic pick-up of the Earth's rotation, which created a preferred direction in its New Jersey lab. The effective signal measured by the atoms was more than 10,000 times larger than the measured Lorentz violating limit.
To overcome this systematic effect, the Romalis Group moved its apparatus to the Cryo facility at the Amundsen-Scott South Pole Station in January 2013. Here, the effects of the Earth's rotation are almost completely suppressed, while improving the test’s precision by two orders of magnitude.
“Polarized atoms in the co-magnetometer are extremely sensitive to rotations,” continued Romalis. “At Princeton, we pick up a large background signal due to Earth's rotation. At the South Pole, we can almost completely eliminate that signal. The South Pole provides the most symmetrical location on Earth to look for the effects of cosmic anisotropy. At Princeton, the Earth’s signal is 2.6 PT—10,000 times larger than the current Lorentz-violating limit. Located 230 meters from the geographic South Pole, the Earth’s signal is less than 0.1 PT, 26,000 times smaller than the Princeton signal.”
(PT—Transverse Momentum—the momentum of an object transverse to the beam axis.)

NEED FOR VIBRATION ISOLATION
The Romalis Group’s atomic spin co-magnetometer, in use both at Princeton University in New Jersey and at its South Pole lab, is among the most sensitive devices for testing Lorentz symmetry. Consequently, precision vibration isolation is required to isolate vibrations from its sensitive components—not only for the co-magnetometer, but for the system’s associated lasers and optical alignments.
Vibrations in the range of few hertz (Hz) to a few 10s of Hz will influence the testing. These internal and external influences primarily cause lower frequency vibrations which are transmitted through the structure, creating strong disturbances in sensitive equipment.
Vibration within this range can be caused by a multitude of factors. Every structure is transmitting noise. Within the building itself, the heating and ventilation system, fans, pumps and elevators are just some of the mechanical devices that create vibration. Depending on how far away the equipment is from these vibration sources, and where in the structure the equipment is located, whether on the third floor or in the basement, for example, will determine how strongly the instrumentation will be influenced.
External to the building, the testing can be influenced by vibrations from vehicle movement, nearby construction, noise from aircraft, and even wind and other weather conditions can cause movement of the structure.
VACUUM-COMPATIBLE, NEGATIVE-STIFFNESS VIBRATION ISOLATION
The Romalis Group selected a Negative-Stiffness vibration isolator, customized to be only mildly magnetic, for its Lorentz symmetry testing, both at Princeton University and at the South Pole.
“A key factor was its ability to isolate vibrations within a vacuum chamber, which houses the co-magnetometer,” explained Romalis. “Air tables cannot isolate vibrations within a vacuum.”
Aside from the vacuum requirement, air systems are usually a less than optimal set-up for cancelling out low Hz vibrations. They do achieve some isolation—usually in one dimension (vertically), and provide limited horizontal isolation. But they do not isolate to the extent that is needed at very low resonance frequencies, the low cycle perturbations frequently come straight through to the equipment.
Developed and patented by Minus K Technology, Negative-Stiffness isolators provide a unique capability, employing a completely mechanical concept in low-frequency vibration isolation, with no air or electricity required.
What is very advantageous about Negative-Stiffness isolators is that they achieve a high level of isolation in multiple directions. Negative-Stiffness isolators have the flexibility of custom tailoring resonant frequencies to 0.5 Hz* vertically and horizontally (with some versions at 1.5 Hz horizontally).
(*Note: For an isolation system with a 0.5 Hz natural frequency, isolation begins at 0.7 Hz and improves with increase in the vibration frequency. The natural frequency is more commonly used to describe the system performance.)
Vertical-motion isolation is provided by a stiff spring that supports a weight load, combined with a Negative-Stiffness mechanism. The net vertical stiffness is made very low without affecting the static load-supporting capability of the spring. Beam-columns connected in series with the vertical-motion isolator provide horizontal-motion isolation. A beam-column behaves as a spring combined with a negative-stiffness mechanism.
VIBRATION TRANSMISSIBILITY
Vibration transmissibility is a measure of the vibrations that are transmitted through the isolator relative to the input vibrations. Negative-Stiffness isolators, when adjusted to 0.5 Hz, achieve approximately 93 percent isolation efficiency at 2 Hz; 99 percent at 5 Hz; and 99.7 percent at 10 Hz. Negative-Stiffness isolators deliver very high performance, as measured by a transmissibility curve.
Negative-Stiffness isolators resonate at 0.5 Hz. At this frequency there is almost no energy present. It would be very unusual to find a significant vibration at 0.5 Hz. Vibrations with frequencies above 0.7 Hz (where negative-stiffness isolators begin isolating) are rapidly attenuated with increases in frequency.
SOUTH POLE FLEXIBILITY
Negative-Stiffness isolators do not require electricity or compressed air. There are no motors, pumps or chambers, and no maintenance because there is nothing to wear out. They operate purely in a passive mechanical mode.
If equipment can be isolated from vibrations without having to deal with compressed air or electricity, then it makes for a system that is simpler to transport, and easier to set-up and maintain. Such was the case with the Romalis Group’s Lorentz symmetry testing at the Amundsen-Scott Station, South Pole.
“The Negative-Stiffness isolator provided the flexibility to be easily transported with our alkali metal-noble gas co-magnetometer from our Princeton lab in New Jersey to the South Pole,” added Romalis. “We did not have to make adjustments for electrical power and pumps to support the vibration isolation.”
Jim McMahon writes on advancements in instrumentation technology. jim.mcmahon@zebracom.net
ADDITIONAL DRAWINGS / PHOTOS


